13 How to choose an estimand: Real-world example
13.1 Comparative effectiveness of two medications for opioid use disorder (OUD)
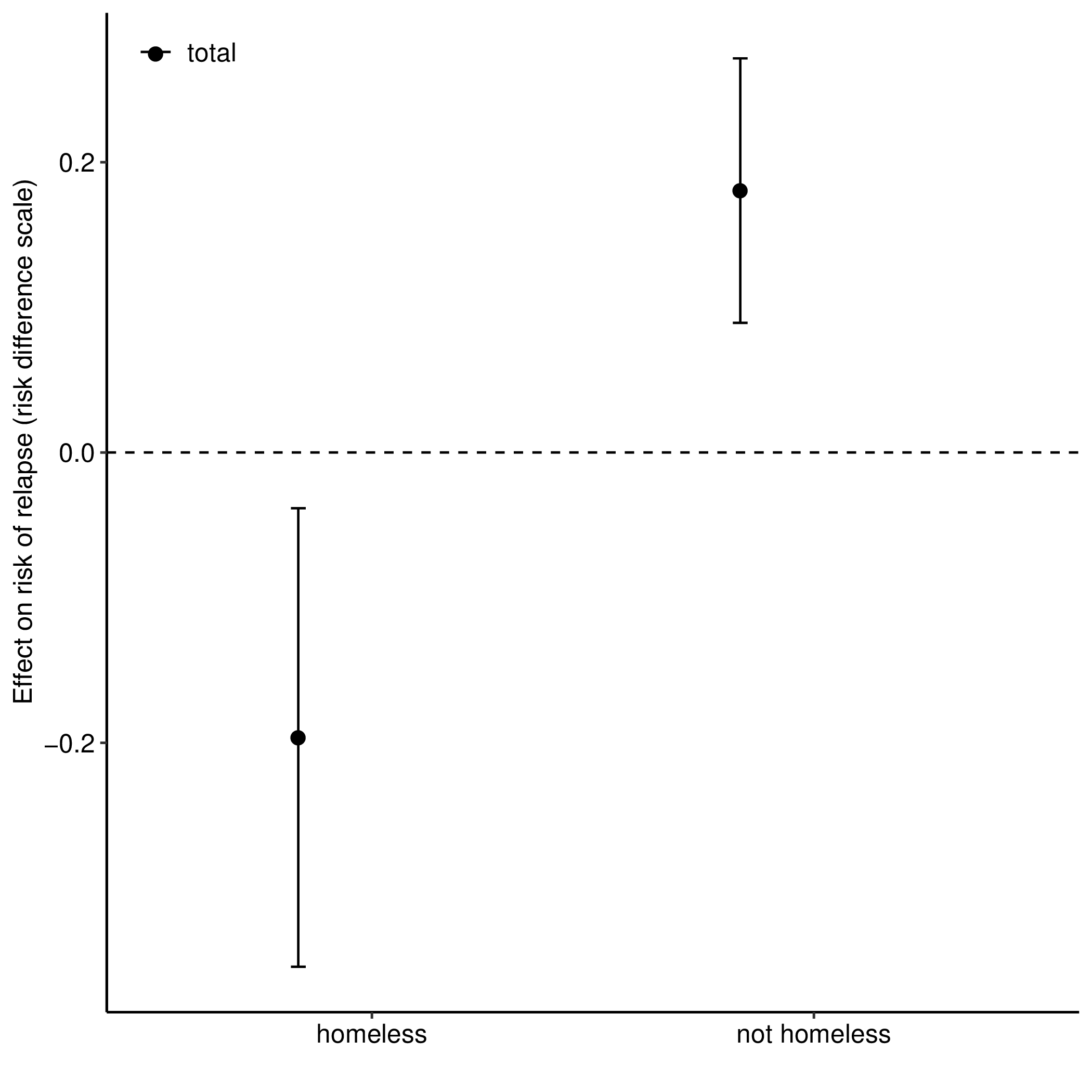
Motivation: Opposite overall treatment effects for homeless versus nonhomeless participants. This application was explored in detail by (1).
13.1.1 Getting specific about the question
To what extent does the indirect effect through mediators of adherence, pain, and depressive symptoms explain the differences in treatment effects on OUD relapse for homeless and nonhomeless individuals?
What estimand do we want?
- Can we set
- Are we interested in estimating indirect effects?
- Do we have an intermediate confounder?
- Yes, and it’s important.
- Do we have a binary treatment assignment variable and a binary intermediate confounder?
- Yes.
- Can we assume monotonicity?
- Yes.
What if we don’t want to assume monotonicity, or if we do not have a binary treatment assignment variable and binary intermediate confounder?
- Do we want to estimate the path through treatment initiation (
- Yes, so, not the conditional versions of these effects.
- Estimands:
- Direct effect:
- Indirect effect:
- Direct effect:
- Here
- Need to incorporate multiple and continuous mediators
What if positivity assumption
- But we can estimate the effect of some stochastic interventions, e.g., IPSIs
- Trade-off between feasibility and interpretation
What if the exposure variable is continuous?
- But we can estimate the effect of some stochastic interventions
- Work in progress (including upcoming R software)