10  “Modern” causal mediation analysis

10.1 Motivating study

• A recent, large, multi-site trial (X:BOT) compared the effectiveness of XR-NTX to buprenorphine–naloxone (BUP-NX) in preventing relapse among those with OUD starting medication in inpatient treatment settings.

• An analysis of potential moderators of medication effectiveness found that homeless individuals had a lower risk of relapse on XR-NTX, whereas non-homeless individuals had a lower risk of relapse on BUP-NX.

• The effect sizes were similarly large for these groups but in opposite directions.

• The underlying mechanisms for these differences have not yet been explored. We can to identify these mechanisms by using mediation analysis.

• We can to use mediation analysis to explore the mechanisms underlying these differences.

• Key questions:

  • Do differences in the effects of treatment (comparing two medications for opioid use disorder, naltrexone v. buprenorphine) on risk of relapse operate through mediators of adherence, opioid use, pain, and depressive symptoms? (1)
  • Are those mediated effects different for homeless vs non-homeless individuals?

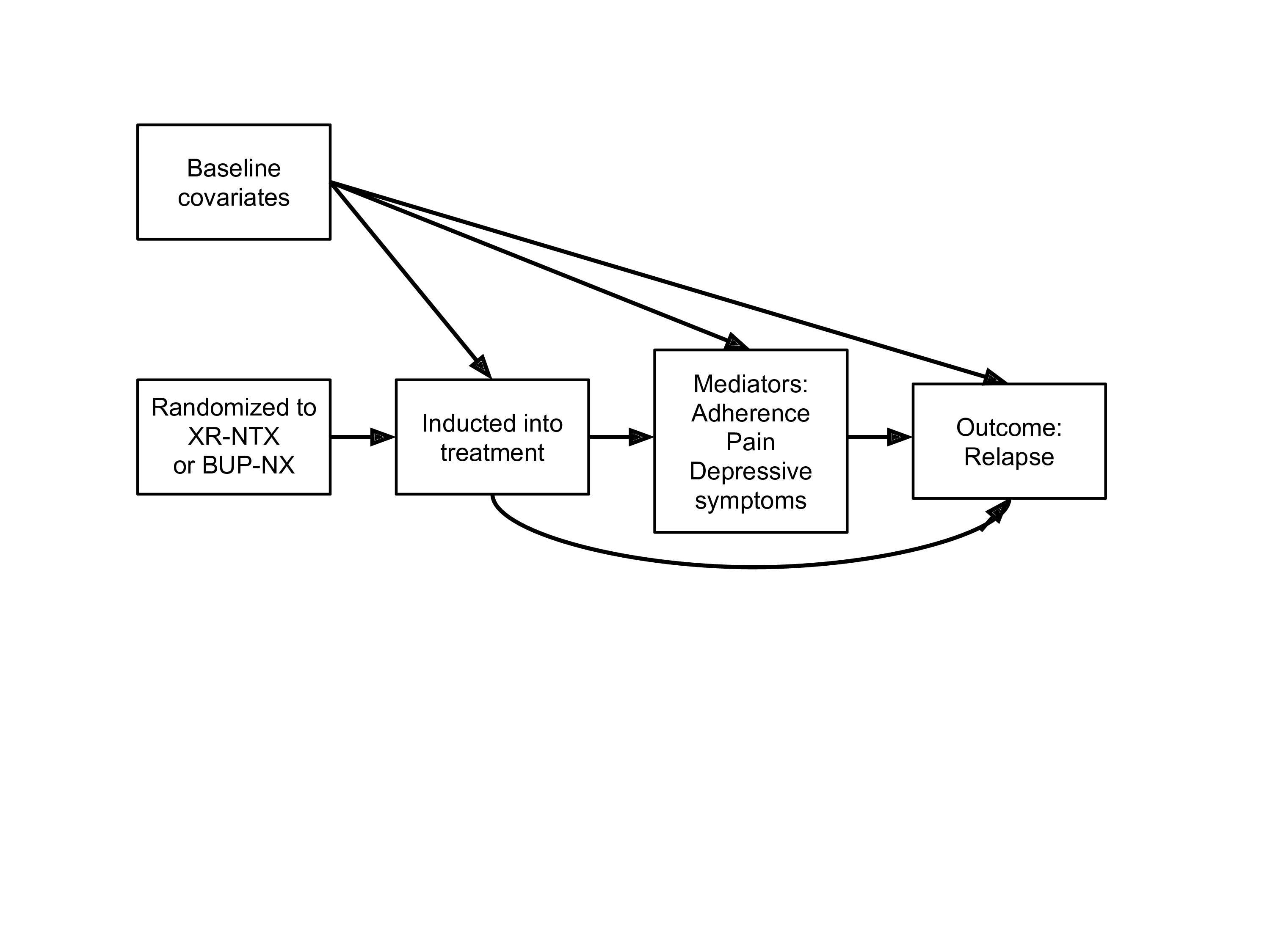
10.2 What is causal mediation analysis?

• Statistical mediation analyses assess associations between the variables. They can help you establish, for example, if the association between treatment and outcome can be mostly explained by an association between treatment and mediator
• Causal mediation analyses, on the other hand, seek to asess causal relations. For example, they help you establish whether treatment causes the outcome because it causes the mediator. To do this, causal mediation seek to understand how the paths behave under circumstances different from the observed circumstances (e.g., interventions)

10.2.1 Why are the causal methods that we will discuss today important?

• Assume you are interested in the effect of treatment assignment \(A\) (naltrexone vs. buprenorphine) on an outcome \(Y\) (risk of relapse) through mediators \(M\) (e.g., opioid use, pain, depressive symptoms)
• We have pre-treatment confounders \(W\)
• There is a confounder \(Z\) of \(M \rightarrow Y\) affected by treatment assignment (with adherence)
• We could fit the following models:

\[ \E(M \mid A=a, W=w, Z=z) & = \gamma_0 + \gamma_1 a + \gamma_2 w + \gamma_3 z \\ \E(Y \mid M=m, A=a, W=w, Z=z) & = \beta_0 + \beta_1 m + \beta_2 a + \beta_3 w + \beta_4 z \]

• The product \(\gamma_1 \beta_1\) has been proposed as a measure of the effect of \(A\) on \(Y\) through \(M\)
• Causal interpretation problems with this method: We will see that this parameter cannot be interpreted as a causal effect

10.2.2 R Example:

• Assume we have a pre-treatment confounder of \(Y\) and \(M\), denote it with \(W\)

• For simplicity, assume \(A\) is randomized

• We’ll generate a really large sample from a data generating mechanism so that we are not concerned with sampling errors

  n <- 1e6
  w <- rnorm(n)
  a <- rbinom(n, 1, 0.5)
  z <- rbinom(n, 1, 0.2 * a + 0.3)
  m <- rnorm(n, w + z)
  y <- rnorm(n, m + w - a + z)

• Note that the indirect effect (i.e., the effect through \(M\)) in this example is nonzero (there is a pathway \(A \rightarrow Z \rightarrow M \rightarrow Y\))

• Let’s see what the product of coefficients method would say:

  lm_y <- lm(y ~ m + a + w + z)
  lm_m <- lm(m ~ a + w + z)
  ## product of coefficients
  coef(lm_y)[2] * coef(lm_m)[2]

  #>             m 
  #> -0.0007092214

Among other things, in this workshop:

• We will provide some understanding for why the above method fails in this example
• We will study estimators that are robust to misspecification in the above models

10.3 Causal mediation models

In this workshop we will use directed acyclic graphs. We will focus on the two types of graph:

10.3.1 No intermediate confounders

10.3.2 Intermediate confounders

The above graphs can be interpreted as a non-parametric structural equation model (NPSEM), also known as structural causal model (SCM):

\[ W & = f_W(U_W) \nonumber \\ A & = f_A(W, U_A) \nonumber \\ Z & = f_Z(W, A, U_Z) \nonumber \\ M & = f_M(W, A, Z, U_M) \nonumber \\ Y & = f_Y(W, A, Z, M, U_Y) \]

• Here \(U=(U_W, U_A, U_Z, U_M, U_Y)\) is a vector of all unmeasured exogenous factors affecting the system
• The functions \(f\) are assumed fixed but unknown
• We posit this model as a system of equations that nature uses to generate the data
• Therefore we leave the functions \(f\) unspecified (i.e., we do not know the true nature mechanisms)
• Sometimes we know something: e.g., if \(A\) is randomized we know \(A=f_A(U_A)\) where \(U_A\) is the flip of a coin (i.e., independent of everything).

10.4 Counterfactuals

• Recall that we are interested in assessing how the pathways would behave under circumstances different from the observed circumstances
• We operationalize this idea using counterfactual random variables
• Counterfactuals are hypothetical random variables that would have been observed in an alternative world where something had happened, possibly contrary to fact

We will use the following counterfactual variables:

• \(Y_a\) is a counterfactual variable in a hypothetical world where \(\P(A=a)=1\) with probability one for some value \(a\)
• \(Y_{a,m}\) is the counterfactual outcome in a world where \(\P(A=a,M=m)=1\)
• \(M_a\) is the counterfactual variable representing the mediator in a world where \(\P(A=a)=1\).

10.4.1 How are counterfactuals defined?

• In the NPSEM framework, counterfactuals are quantities derived from the model.

• Once you define a change to the causal system, that change needs to be propagated downstream.

  • Example: modifying the system to make everyone receive XR-NTX yields counterfactual adherence, mediators, and outcomes.

• Take as example the DAG in Figure 1.2:

  \[ A &= a \nonumber \\ Z_a &= f_Z(W, a, U_Z) \nonumber \\ M_a &= f_M(W, a, Z_a, U_M) \nonumber \\ Y_a &= f_Y(W, a, Z_a, M_a, U_Y) \]

• We will also be interested in joint changes to the system:

  \[ A &= a \nonumber \\ Z_a &= f_Z(W, a, U_Z) \nonumber \\ M &= m \nonumber \\ Y_{a,m} &= f_Y(W, a, Z_a, m, U_Y) \]

• And, perhaps more importantly, we will use nested counterfactuals

• For example, if \(A\) is binary, you can think of the following counterfactual

  \[ A &= 1 \nonumber \\ Z_1 &= f_Z(W, 1, U_Z) \nonumber \\ M &= M_0 \nonumber \\ Y_{1, M_0} &= f_Y(W, 1, Z_1, M_0, U_Y) \]

• \(Y_{1, M_0}\) is interpreted as the outcome for an individual in a hypothetical world where treatment was given but the mediator was held at the value it would have taken under no treatment.

• Causal mediation effects are often defined in terms of the distribution of these nested counterfactuals.

• That is, causal effects give you information about what would have happened in some hypothetical world where the mediator and treatment mechanisms changed.

1.

Rudolph K, Diaz I, Hejazi N, van der Laan M, Luo S, Shulman M, Campbell A, Rotrosen J, Nunes E. Explaining differential effects of medication for opioid use disorder using a novel approach incorporating mediating variables. Addiction Wiley Online Library; 2020;