Appendix A — Appendix: Stochastic direct and indirect effects

A.1 Definition of the effects

Consider the following directed acyclic graph.

A.2 Motivation for stochastic interventions

• So far we have discussed controlled, natural, and interventional (in)direct effects
• These effects require that \(0 < \P(A=1\mid W) < 1\)
• They are defined only for binary exposures
• What can we do when the positivity assumption does not hold or the exposure is continuous?
• Solution: We can use stochastic effects

A.3 Definition of stochastic effects

There are two possible ways of defining stochastic effects:

• Consider the effect of an intervention where the exposure is drawn from a distribution
  • For example incremental propensity score interventions
• Consider the effect of an intervention where the post-intervention exposure is a function of the actually received exposure
  • For example modified treatment policies
• In both cases \(A \mid W\) is a non-deterministic intervention, thus the name stochastic intervention

A.3.1 Example: incremental propensity score interventions (IPSI)

See (1)

Definition of the intervention

• Assume \(A\) is binary, and \(\P(A=1\mid W=w) = g(1\mid w)\) is the propensity score
• Consider an intervention in which each individual receives the intervention with probability \(g_\delta(1\mid w)\), equal to \[\begin{equation*} g_\delta(1\mid w)=\frac{\delta g(1\mid w)}{\delta g(1\mid w) + 1 - g(1\mid w)} \end{equation*}\]
• e.g., draw the post-intervention exposure from a Bernoulli variable with probability \(g_\delta(1\mid w)\)
• The value \(\delta\) is user given
• Let \(A_\delta\) denote the post-intervention exposure distribution
• Some algebra shows that \(\delta\) is an odds ratio comparing the pre- and post-intervention exposure distributions \[\begin{equation*} \delta = \frac{\text{odds}(A_\delta = 1\mid W=w)} {\text{odds}(A = 1\mid W=w)} \end{equation*}\]
• Interpretation: what would happen in a world where the odds of receiving treatment is increased by \(\delta\)
• Let \(Y_{A_\delta}\) denote the outcome in this hypothetical world

A.3.1.1 Illustrative application for IPSIs

• Consider the effect of participation in sports on children’s BMI
• Mediation through snacking, exercising, etc.
• Intervention: for each individual, increase the odds of participating in sports by \(\delta=2\)
• The post-intervention exposure is a draw \(A_\delta\) from a Bernoulli distribution with probability \(g_\delta(1\mid w)\)

A.3.2 Example: modified treatment policies (MTP)

See (2)

Definition of the intervention

• Consider a continuous exposure \(A\) taking values in the real numbers
• Consider an intervention that assigns exposure as \(A_\delta = A - \delta\)
• Example: \(A\) is pollution measured as \(PM_{2.5}\) and you are interested in an intervention that reduces \(PM_{2.5}\) concentration by some amount \(\delta\)

A.3.3 Mediation analysis for stochastic interventions

• The total effect of an IPSI can be computed as a contrast of the outcome under intervention vs no intervention:

\[ \psi = \E[Y_{A_\delta} - Y] \]

• Recall the NPSEM

\[ W & = f_W(U_W)\\ A & = f_A(W, U_A)\\ M & = f_M(W, A, U_M)\\ Y & = f_Y(W, A, M, U_Y) \]

• From this we have

\[ M_{A_\delta} & = f_M(W, A_\delta, U_M)\\ Y_{A_\delta} & = f_Y(W, A_\delta, M_{A_\delta}, U_Y) \]

• Thus, we have \(Y_{A_\delta} = Y_{A_\delta, M_{A_\delta}}\) and \(Y = Y_{A,M_{A}}\)

• Let us introduce the counterfactual \(Y_{A_\delta, M}\), interpreted as the outcome observed in a world where the intervention on \(A\) is performed but the mediator is fixed at the value it would have taken under no intervention:

\[[Y_{A_\delta, M} = f_Y(W, A_\delta, M, U_Y)]\]

• Then we can decompose the total effect into:

\[ \E[Y&_{A_\delta,M_{A_\delta}} - Y_{A,M_A}] = \\ &\underbrace{\E[Y_{\color{red}{A_\delta},\color{blue}{M_{A_\delta}}} - Y_{\color{red}{A_\delta},\color{blue}{M}}]}_{\text{stochastic natural indirect effect}} + \underbrace{\E[Y_{\color{blue}{A_\delta},\color{red}{M}} - Y_{\color{blue}{A},\color{red}{M}}]}_{\text{stochastic natural direct effect}} \]

A.4 Identification assumptions

• Confounder assumptions:
  • \(A \indep Y_{a,m} \mid W\)
  • \(M \indep Y_{a,m} \mid W, A\)
• No confounder of \(M\rightarrow Y\) affected by \(A\)
• Positivity assumptions:
  • If \(g_\delta(a \mid w)>0\) then \(g(a \mid w)>0\)
  • If \(\P(M=m\mid W=w)>0\) then \(\P(M=m\mid A=a,W=w)>0\)

Under these assumptions, stochastic effects are identified as follows

• The indirect effect can be identified as follows

\[ \E&(Y_{A_\delta} - Y_{A_\delta, M}) =\\ &\E\left[\color{Goldenrod}{\sum_{a}\color{ForestGreen}{\{\E(Y\mid A=a, W) -\E(Y\mid A=a, M, W)\}}g_\delta(a\mid W)}\right] \]

• The direct effect can be identified as follows

\[ \E&(Y_{A_\delta} - Y_{A_\delta, M}) =\\ &\E\left[\color{Goldenrod}{\sum_{a}\color{ForestGreen}{\{\E(Y\mid A=a, M, W) - Y\}}g_\delta(a\mid W)}\right] \]

• Let’s dissect the formula for the indirect effect in R:

  n <- 1e6
  w <- rnorm(n)
  a <- rbinom(n, 1, plogis(1 + w))
  m <- rnorm(n, w + a)
  y <- rnorm(n, w + a + m)

• First, fit regressions of the outcome on \((A,W)\) and \((M,A,W)\):

  fit_y1 <- lm(y ~ m + a + w)
  fit_y2 <- lm(y ~ a + w)

• Get predictions fixing \(A=a\) for all possible values \(a\)

  pred_y1_a1 <- predict(fit_y1, newdata = data.frame(a = 1, m, w))
  pred_y1_a0 <- predict(fit_y1, newdata = data.frame(a = 0, m, w))
  pred_y2_a1 <- predict(fit_y2, newdata = data.frame(a = 1, w))
  pred_y2_a0 <- predict(fit_y2, newdata = data.frame(a = 0, w))

• Compute [] for each value \(a\)

  pseudo_a1 <- pred_y2_a1 - pred_y1_a1
  pseudo_a0 <- pred_y2_a0 - pred_y1_a0

• Estimate the propensity score \(g(1\mid w)\) and evaluate the post-intervention propensity score \(g_\delta(1\mid w)\)

  pscore_fit <- glm(a ~ w, family = binomial())
  pscore <- predict(pscore_fit, type = 'response')
  ## How do the intervention vs observed propensity score compare
  pscore_delta <- 2 * pscore / (2 * pscore + 1 - pscore)

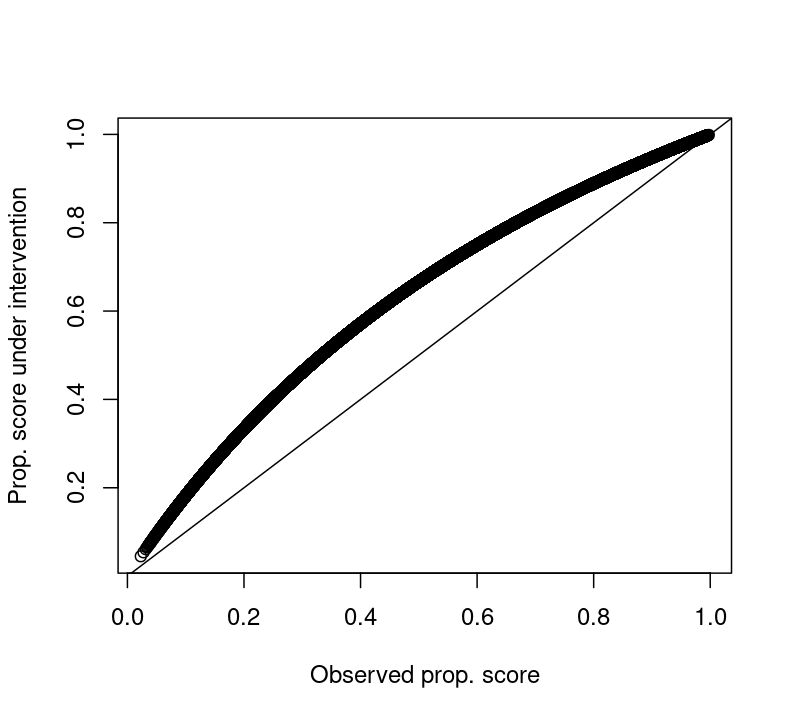
• What do the post-intervention propensity scores look like?

  plot(pscore, pscore_delta, xlab = 'Observed prop. score',
       ylab = 'Prop. score under intervention')
  abline(0, 1)

  

A.5 What are the odds of exposure under intervention vs real world?

odds <- (pscore_delta / (1 - pscore_delta)) / (pscore / (1 - pscore))
summary(odds)

#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>       2       2       2       2       2       2

• Compute the sum

\[ \color{Goldenrod}{\sum_{a}\color{ForestGreen}{\{\E(Y\mid A=a, W) - \E(Y\mid A=a, M, W)\}}g_\delta(a\mid W)} \]

indirect <- pseudo_a1 * pscore_delta + pseudo_a0 * (1 - pscore_delta)

• The average of this value is the indirect effect

  ## E[Y(Adelta) - Y(Adelta, M)]
  mean(indirect)

  #> [1] 0.1092928

• The direct effect is

\[ \E&(Y_{A_\delta} - Y_{A_\delta, M}) =\\ &\E\left[\color{Goldenrod}{\sum_{a}\color{ForestGreen}{\{\E(Y\mid A=a, M, W) - Y\}}g_\delta(a\mid W)}\right] \]

• Which can be computed as

  direct <- (pred_y1_a1 - y) * pscore_delta +
         (pred_y1_a0 - y) * (1 - pscore_delta)
  mean(direct)

  #> [1] 0.1092246

A.6 Summary

• Stochastic (in)direct effects
  • Relax the positivity assumption
  • Can be defined for non-binary exposures
  • Do not require a cross-world assumption
• Still require the absence of intermediate confounders
  • But, compared to the NDE and NIE, we can design a randomized study where identifiability assumptions hold, at least in principle
  • There is a version of these effects that can accommodate intermediate confounders (3)
  • R implementation to be released soon…stay tuned!

1.

Kennedy EH. Nonparametric causal effects based on incremental propensity score interventions. Journal of the American Statistical Association Taylor & Francis; 2018;

2.

Dı́az I, Hejazi NS. Causal mediation analysis for stochastic interventions. Journal of the Royal Statistical Society: Series B (Statistical Methodology) Wiley Online Library; 2020;82:661–83.

3.

Hejazi NS, Rudolph KE, Laan MJ van der, Dı́az I. Nonparametric causal mediation analysis for stochastic interventional (in) direct effects. Biostatistics [Internet] Oxford University Press; 2022;(in press). Available from: https://arxiv.org/abs/2009.06203